СОДЕРЖАНИЕ Введение. 3 1 Статистические методы управления процессами. 5 1.1 Применение статистических инструментов контроля качества при производстве и контроле качества продукции. 5 1.2 Роль корреляционно – регрессионного анализа в обработке. 7 экономических данных. 7 1.3 Корреляционно-регрессионный анализ и его возможности. 9 2 Особенности производства творога. 18 2.1 Описание технологического процесса производства творога. 18 2.2 Обеспечение качества и безопасности творога. 23 2.3 Возможные виды несоответствий при изготовлении творога. 26 3 Практическая часть. 30 Заключение. 33 Список использованных источников. 34 Введение Молочная промышленность является одной из важнейших отраслей агропромышленного комплекса по обеспечению населения продовольствием. Кисломолочные продукты имеют большое значение в питании человека благодаря лечебным и диетическим свойствам, приятному вкусу, легкой усвояемости. Творог является одним из самых древних кисломолочных продуктов, который римский философ Колумелла еще в I веке нашей эры назвал "желательным блюдом на столах богатых и бедных". Сейчас творог часто называют пищей, не знающей запретов. Творог одинаково рекомендуется и здоровым и больным, и старикам и детям. Творог — продукт, полноценный по биологическому составу, хорошо усваивается. Значительная роль творога в рациональном питании объясняется его составом. Прежде всего ценность творога заключается в большом и полном наборе незаменимых аминокислот, содержании в нем белка, минеральных веществ, в том числе многих микроэлементов, молочного сахара. В твороге имеются и различные витамины. На качество творога могут влиять множество факторов, таких как не соблюдения правильного технологического режима производства, гигиенические требования персонала и оборудования, условия хранения.
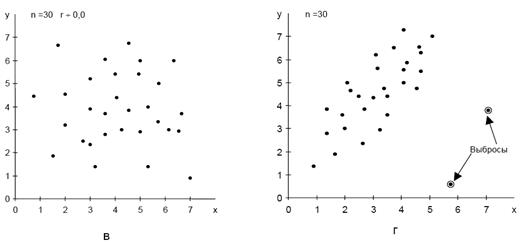
Более эффективный подход при производстве творога, основанный на предупреждении производства непригодной продукции и позволяющий избежать необоснованных потерь. Это может быть достигнуто применением регрессионногоъ анализа для определения причины появления дефектов у творога и нахождения способа их исправления. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. 1 Статистические методы управления процессами 1.1 Применение статистических инструментов контроля качества при производстве и контроле качества продукции Статистические методы играют важную роль в объективной оценке количественных и качественных характеристик процесса и являются одним из важнейших элементов системы обеспечения качества продукции и всего процесса управления качеством. Неслучайно основоположник современной теории менеджмента качества Э. Деминг придавал огромное значение статистическим методам. Качество продукции закладывается в процессе научных исследований, конструкторских и технологических разработок, обеспечивается хорошей организацией производства и, наконец, оно поддерживается в процессе эксплуатации или потребления. На всех этих этапах важно осуществлять своевременный контроль и получать достоверную оценку качества продукции. Для уменьшения затрат и достижения уровня качества, удовлетворяющего потребителя, нужны методы, направленные не на устранение дефектов (несоответствий) готовой продукции, а на предупреждение причин их появления в процессе производства. Проблемами сбора, обработки и анализа результатов производственной деятельности занимается математическая статистика, которая включает в себя большое количество не только известных методов, но и современных инструментов анализа и выявления дефектов. К таким методам можно отнести корреляционный и регрессионный анализы, проверку статистических гипотез, факторный анализ, анализ временных рядов, анализ безотказности и т. д. Большое распространение в управлении качеством (под влиянием японских специалистов) получили семь простых методов, применение которых не требует высокой квалификации персонала и позволяет охватить анализ причины большинства возникающих на производстве дефектов. Семь основных инструментов контроля качества — набор инструментов, позволяющих облегчить задачу контроля протекающих процессов и предоставить различного рода факты для анализа, корректировки и улучшения качества процессов. Контрольный листок — инструмент для сбора данных и их автоматического упорядочения для облегчения дальнейшего использования собранной информации. Гистограмма — инструмент, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания данных в определенный (заранее заданный) интервал. Диаграмма Парето — инструмент, позволяющий объективно представить и выявить основные факторы, влияющие на исследуемую проблему, и распределить усилия для ее эффективного разрешения. Метод стратификации (расслаивания данных) — инструмент, позволяющий произвести разделение данных на подгруппы по определенному признаку. Диаграмма разброса (рассеивания) — инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных. Диаграмма Исикавы (причинно – следственная диаграмма) — инструмент, который позволяет выявить наиболее существенные факторы (причины), влияющие на конечный результат (следствие). Контрольная карта — инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявленных к процессу требований. Во многих отраслях экономики невозможно корректное решение многих проблем без применения статистических зависимостей между исследуемыми факторами. Это вызвано тем, что подавляющеечисло взаимосвязей между величинами имеет не функциональный, а случайный характер. Так, например, объем продаж продукции невозможно точно прогнозировать с изменением цены, производительность обработки заготовок на станках вероятностно зависит от режимов резания, качество шлифованных поверхностей так же с какой-то долей вероятности определяется величиной зернистости абразивного инструмента и т. д. Практически вся эконометрия зиждется на статистических зависимостях 1.2 Роль корреляционно – регрессионного анализа в обработке экономических данных Корреляционный анализ и регрессионный анализ являются смежными разделами математической статистики, и предназначаются для изучения по выборочным данным статистической зависимости ряда величин; некоторые из которых являются случайными. При статистической зависимости величины не связаны функционально, но как случайные величины заданы совместным распределением вероятностей. Формально корреляционная модель взаимосвязи системы случайных величин Статистические данные почти всегда представлены в виде таблиц. Числовые данные, содержащиеся в таблицах, обычно имеют между собой явные (известные) или неявные (скрытые) связи. Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам. Например, проценты выполнения плана, уровни, удельные веса, отклонения в сумме, отклонения в процентах, темпы роста, темпы прироста, индексы и т. д. Связи же второго типа (неявные) заранее неизвестны. Однако необходимо уметь объяснять и предсказывать (прогнозировать) сложные явления для того, чтобы управлять ими. Поэтому специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т.е. математически смоделировать явления или процессы. Одну из таких возможностей предоставляет корреляционно-регрессионный анализ. Математические модели строятся и используются для трех обобщенных целей: • для объяснения; • для предсказания; • для управления. Пользуясь методами корреляционно-регрессионного анализа, аналитики измеряют тесноту связей показателей с помощью коэффициента корреляции. При этом обнаруживаются связи, различные по силе (сильные, слабые, умеренные и др.) и различные по направлению (прямые, обратные). Если связи окажутся существенными, то целесообразно будет найти их математическое выражение в виде регрессионной модели и оценить статистическую значимость модели. Как правило, значимое уравнение используется, для прогнозирования изучаемого явления или показателя. Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Таким образом, регрессионные вычисления и подбор хороших уравнений – это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (маркетинг, торговля, медицина и т. д.). Усвоив технологию использования этого инструмента, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность. Корреляционно-регрессионный анализ считается одним из главных математическим и графическим моделированием трендов (тенденций). Широко применяются как однофакторные, так и множественные регрессионные модели. 1.3 Корреляционно-регрессионный анализ и его возможностиКорреляционный анализ является одним из методов статистического анализа взаимосвязи нескольких признаков. Он определяется как метод, применяемый тогда, когда данные наблюдения можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону. Основная задача корреляционного анализа (являющаяся основной и в регрессионном анализе) состоит в оценке уравнения регрессии. Корреляция – это статистическая зависимость между случайными величинами, не имющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. 1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными). 2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков. 3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование. В задачи корреляционного анализа входит: -установление направления (положительное или отрицательное) и формы (линейная или нелинейная) связи между варьирующими признаками, -измерение тесноты связи (значения коэффициентов корреляции), -проверка уровня значимости коэффициентов корреляции. Диаграмма рассеивания (рисунок 1) применяется для выяснения зависимости одной переменной величины (показателя качества продукции, параметра технологического процесса, величины затрат на качество и т.п.) от другой. Например: -характеристика качества и влияющий на нее фактор; -две различные, но связанные между собой характеристики качества; -два фактора, влияющие на одну характеристику качества.
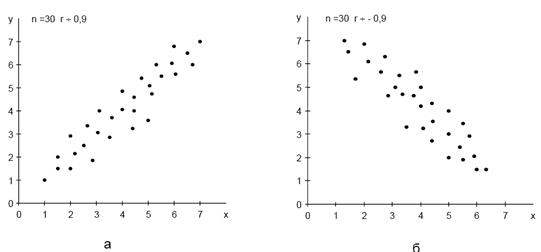
Рисунок 1. Диаграмма рассеивания Виды корреляционных связей между измеренными признаками могут быть линейными и нелинейными, положительными или отрицательными. Варианты корреляционных связей отражены на рисунке 2 (а – г).Возможна также ситуация, когда между переменными невозможно установить какую-либо зависимость (рисунок 2 – в). В этом случае говорят об отсутствии корреляционной связи. С целью выявления характеристик корреляционных зависимостей применяют корреляционный анализ. Прежде чем начать исследование парной стохастической зависимости, необходимо убедиться, что массив данных характеризует наличие только двух переменных, корреляционные связи которых надо раскрыть. То есть надо проанализировать собранную информацию на предмет расслоения данных измерения, проверить возможность вмешательства в одну из переменных дополнительного стратифицирующего фактора.
Рисунок 2. Диаграммы рассеяния: а) положительная корреляция, б) отрицательная корреляция, в) корреляция отсутствует, г) выбросы измерений из поля корреляции Определение коэффициента корреляции. Теснота связи количественно выражается величиной коэффициентов корреляции. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определить «полезность» факторных признаков при построении уравнений множественной регрессии. Величина коэффициентов корреляции служит также оценкой соответствия уравнению регрессии выявленным причинно-следственным связям. Первоначально исследования корреляции проводились в биологии, а позднее распространились и на другие области, в том числе на социально-экономическую. Одновременно с корреляцией начала использоваться и регрессия. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. И корреляция, и регрессия служат для установления соотношений между явлениями и для определения наличия или отсутствия связи между ними. Для характеристики тесноты связи между двумя переменными обычно пользуются выборочным парным коэффициентом
При малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по следующей формуле:
Величина коэффициента корреляции изменяется в интервале При Если коэффициент корреляции находится в интервале Если каждая пара значений величин X иY чаще всего одновременно оказывается выше (ниже) соответствующих средних значений, то между величинами существует прямая корреляционная связь и коэффициент корреляции находится в интервале Если же отклонение величины X от среднего значения одинаково часто вызывают отклонения величины Y вниз от среднего значения и при этом отклонения оказываются все время различными, то можно предполагать, что значение коэффициента корреляции стремится к нулю. Следует отметить, что значение коэффициента корреляции не зависит от единиц измерения и выбора начала отсчета. Это означает, что если переменные X иY уменьшить (увеличить) в К раз либо на одно и то же число С , то коэффициент корреляции не изменится. Определение уравнений регрессии. Корреляционную зависимость между переменными X и Y можно выразить с помощью уравнений типа:
которые называются уравнениями регрессии . В этих уравнениях Графическое выражение регрессионного уравнения называют линией регрессии. Предположи, что связь между переменными линейная (рисунок 3), тогда соответствующая регрессионная модель имеет вид:
В уравнении (5) наоборот x – зависимая переменная, а Y – независимая,
Рисунок 3. Парная линейная регрессия. Количественное установление связи (зависимости) между X и Y (или между Y и X ) называется регрессионным анализом. Главная задача регрессионного анализа состоит: · в определение коэффициентов · в определение уровня значимости полученных уравнений регрессии связывающих между собой переменные X и Y. Коэффициент регрессии
Если коэффициент корреляции не известен, коэффициент регрессии можно вычислить по следующей формуле:
Свободный член уравнений регрессии
Вычисление по формулам (6) – (8) достаточно трудоемко, поэтому в регрессионном анализе используют метод наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), т. е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных
Для нахождения минимума данной функции приравниваем к нулю ее частные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Решив эту систему в общем виде, получим:
Проверка значимости коэффициентов регрессии. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n<30) осуществляют с помощью t – критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t – критерия: для параметра
для параметра
где n– объем выборки;
По формуле (14) находится среднее квадратическое отклонение результативного признака y от выравниваемых значений
По формуле (15) рассчитывается среднее квадратическое отклонение факторного признака x от общей средней Вычисленные по формулам (12) и (13) значения, сравниваются с критическим t , которые определяют по таблице Стьюдента с учетом принятого уровня значимости Для оценки значимости коэффициента корреляции r используют тоже критерий t – Стьюдента, который применяется для t – распределения, отличном от нормального. При линейной связи t – критерий можно рассчитать по формуле:
где ( n – 2) – число степеней свободы при заданном уровне значимости Полученное значение 2 Особенности производства творога 2.1 Описание технологического процесса производства творогаТворог – белковый кисломолочный продукт, пищевая и биологическая ценность которого обусловлена высоким содержанием белков, а также серосодержащих аминокислот, которые необходимы человеку для лучшей работы печени и почек. Повышенное содержание минеральных веществ (Са, Р, Fе, Мg и др.) содержатся в идеальном соотношении для усвоения организмом [2]. Продукт в зависимости от молочного сырья подразделяют: 1) из натурального молока; 2) из нормализованного молока; 3) из восстановленного молока; 4) из рекомбинированного молока; 5) из их смесей. Продукт (кроме «из натурального молока») в зависимости от массовой доли, подразделяют на творог: обезжиренный; нежирный; классический;жирный. Схема производства творога традиционным способом представлена на рисунке 4.
Рисунок 4. Технологическая схема производства творога традиционным способом Технологический процесс производства творога традиционным способом состоит из следующих операций: приемка молока, охлаждение, резервирование, подогрев, очистка молока, сепарирование, пастеризация, охлаждение, заквашивание, сквашивание, образование сгустка, обработка сгустка, расфасовка и хранение. Молоко охлаждается до 4 °С для предотвращения развития микрофлоры и порчи молока. Резервирование молока происходит не более 8 часов, для непрерывной работы предприятия. Подогрев происходит до (40…45) °С, осуществляется для уменьшения вязкости молока а также для перевода тугоплавкой фракции жира в жидкое состояние, что в последствии улучшает процесс очистки и отделения сливок. Очищают молоко от механических смесей. В процессе сепарирования производится нормализация молока по жиру и отделение сливок. Расчеты по нормализации молока ведут с учетом содержания в нем белка и проводят, как правило, путем смешивания. Режим пастеризации молока влияет на плотность получаемого при сквашивании сгустка. С увеличением температуры пастеризации плотность сгустка возрастает, но одновременно с этим возрастает и способность сгустка удерживать влагу, что затрудняет удаление из него сыворотки. В связи с этим при выработке творога молоко пастеризуют при температуре (78 ± 2) °С с выдержкой 15 – 20 с. Этот режим считается достаточным для уничтожения микрофлоры в нормализованной смеси и получения сгустка, удобного для дальнейшей обработки. Пастеризованную смесь охлаждают до температуры заквашивания (28…30) °С (в теплое время года) и (30…32) °С (в холодное время года). Заквашивание и сквашивание смеси производят в специальных двустенных ваннах для выработки творога При выработке жирного или полужирного творога кислотным способом в нормализованную смесь вносят закваску, приготовленную на чистых культурах мезофильного молочнокислого стрептококка в количестве до 5 %. Тщательно перемешанное молоко оставляют в состоянии покоя до образования сгустка. Готовность сгустка можно определить пробой на излом, обращая при этом внимание на цвет выделяющейся сыворотки. Более точно окончание сквашивания определяют по кислотности сгустка, которая достигает (70…80) °С. Образование сгустка происходит за 7…9 часов. Готовый сгусток разрезают ножами на кубики с размером по ребру 20 мм и оставляют в покое на 10…15 минут для частичного выделения из него сыворотки, а следовательно, некоторого уплотнения кусочков сгустка. Сыворотка из сгустка, полученного кислотным способом, выделяется медленнее, чем при кислотно-сычужном способе. Для ускорения явления синерезиса в этом случае применяют повышение температуры, что вызывает более сильное стягивание белкового сгустка и более интенсивное выделение из него сыворотки. С этой целью разрезанный и несколько уплотнившийся сгусток нагревают до температуры (40…44) °С, направляя в межстенное пространство ванны горячую воду. Для равномерного нагревания всей массы сгусток осторожно перемешивают. При этом не допускается интенсивное перемешивание, которое вызывает раздробление кусочков сгустка с образованием мелких белковых частиц, которые отойдут с сывороткой, уменьшив при этом выход продукта. Нельзя также допускать перегрев сгустка выше установленной температуры, что способствует получению творога с сухой и грубой консистенцией. При недогреве сгустка в нем замедляется отделение сыворотки, и в результате творог будет иметь повышенную кислотность, мажущуюся консистенцию и увеличатся потери при его производстве. После нагрева сгустка до необходимой температуры его оставляют в покое на 20…30 минут для лучшего обезвоживания. Выделившуюся при этом сыворотку удаляют из ванны Для улучшения выделения сыворотки сгусток прессуют небольшими порциями, помещенными в прочные бязевые или лавсановые мешки. Через штуцер ванны в каждый мешок поступает самотеком по 7…9 кг сгустка. Мешки завязывают и укладывают несколькими рядами в пресс-тележку, где под действием собственного веса из сгустка выделяется сыворотка. Самопрессование происходит в цехе при температуре воздуха не выше 16 °С и продолжается не менее часа. Окончание самопрессования определяют визуально по поверхности сгустка, которая теряет блеск и становится матовой. После самопрессования мешки укладывают в несколько рядов в пресс-тележку или пресс другого типа и под давлением прессуют творог до готовности. Давление при прессовании следует увеличивать постепенно, иначе часть сухих веществ перейдет в сыворотку, и возрастут потери. В процессе прессования мешки с творогом несколько раз встряхивают и перекладывают, чем ускоряют выделение сыворотки. Во избежание повышения кислотности прессование проводят в помещениях с температурой воздуха от 3 до 8 °С. Окончание прессования определяют по содержанию влаги творога. Весь процесс прессования продолжается не более десяти часов. Более целесообразно прессовать творог не в бязевых, а в лавсановых мешках. Это ускоряет отделение сыворотки, в результате продолжительность прессования сокращается на сорок процентов. В связи с этим кислотность творога понижается на (12…15) °Т, что повышает качество готового продукта. Благодаря уменьшению прилипания белкового сгустка к лавсановой ткани потери творога при производстве снижены в пределах 8…10 кг на 1 т продукта. Лавсановую ткань также легче мыть, она значительно прочнее бязи. После прессования творог немедленно направляют на охлаждение до температуры (8…15) °С, используя для этого охладители различных конструкций, наиболее совершенными среди которых являются двухцилиндровые закрытые охладители [1]. 2.2 Обеспечение качества и безопасности творогаГосударственной думой 23 мая 2008 года был принят ФЗ № 88 Российской Федерации «Технический регламент на молоко и молочную продукцию», который устанавливает требования к производству, маркировке и хранению молока и молочной продукции. Творог — кисломолочный продукт, произведенный с использованием заквасочных микроорганизмов — лактококков или смеси лактококков и термофильных молочнокислых стрептококков и методов кислотной или кислотно-сычужной коагуляции белков с последующим удалением сыворотки путем самопрессования, прессования, центрифугирования и (или) ультрафильтрации. Требования органолептических характеристик, по ФЗ № 88 РФ «Технический регламент на молоко и молочную продукцию», которым должен соответствовать творог, приведены в таблица 1. Таблица 1 – Органолептические характеристики творога
Также в техническом регламенте имеются физико-химические показатели качества творога, которые представлены в таблице 2 [5]. Таблица 2 – Физико-химические показатели качества творога
Требования к безопасности сырого молока . Условия получения от сельскохозяйственных животных молока, перевозки, реализации и утилизации сырого молока и сырых сливок, молочных продуктов непромышленного производства должны соответствовать требованиям законодательства Российской Федерации о ветеринарии [5]. Сырое молоко должно быть получено от здоровых сельскохозяйственных животных на территории, благополучной в отношении инфекционных и других общих для человека и животных заболеваний. Не допускается использование в пищу сырого молока, полученного в течение первых семи дней после дня отела животных и в течение пяти дней до дня их запуска (перед их отелом) и (или) от больных животных и находящихся на карантине животных. Изготовитель должен обеспечивать безопасность сырого молока в целях отсутствия в нем остаточных количеств ингибирующих, моющих, дезинфицирующих и нейтрализующих веществ, стимуляторов роста животных (в том числе гормональных препаратов), лекарственных средств (в том числе антибиотиков), применяемых в животноводстве в целях откорма, лечения скота и (или) профилактики его заболеваний. Молоко, получаемое от разных видов сельскохозяйственных животных, за исключением коровьего молока, должно соответствовать показателям, установленным техническим регламентом. Показатели микробиологической безопасности и содержания соматических клеток коровьего сырого молока и сырых сливок не должны превышать установленный допустимый уровень Федерального закона [5]. Требования к упаковке молока и продуктов его переработки . Молоко и продукты его переработки, предназначенные для реализации, должны быть расфасованы, упакованы в тару и (или) упаковки, изготовленные из экологически безопасных материалов, разрешенных федеральным органом исполнительной власти, осуществляющим функции по контролю и надзору в сфере обеспечения санитарно-эпидемиологического благополучия населения, защиты прав потребителей, для контакта с пищевыми продуктами и обеспечивающих безопасность и качество молока и продуктов его переработки в течение срока их годности [5]. Не допускается использование тары потребителя (покупателя) при реализации нерасфасованных и неупакованных скоропортящихся продуктов переработки молока. Нарезанные продукты переработки молока упаковываются изготовителем или продавцом в условиях, обеспечивающих безопасность таких продуктов и сохранение их органолептических свойств. Каждая упаковка продуктов переработки молока должна иметь маркировку, этикетку и при необходимости листок-вкладыш или ярлык, содержащие информацию для потребителей в соответствии со статьей 36 « Технического регламента на молоко и молочную продукцию». Продукты переработки молока, находящиеся в поврежденной таре и (или) упаковке, подлежат отзыву. 2.3 Возможные виды несоответствий при изготовлении творогаДефекты творога вызываются неправильным ведением технологического процесса и нарушением условий хранения. В таблице 3 представлены все дефекты, причины их возникновения, методы их предупреждения [8]. Таблица 3 – Дефекты творога
Дефекты или пороки творога могут возникать на различных стадиях технологического процесса. Например, кормовой вкус зависит от качества молока, на стадии его приемки. Прогорклый вкус может возникнуть на стадии пастеризации молока. Температуру пастеризации устанавливают с таким расчетом, чтобы инактивировать фермент липазу, при наличии которой возникает прогорклый вкус при длительном хранении творога, а также уничтожить термофильные молочнокислые палочки, вызывающие перекисание творога в период хранения, и по возможности полнее осадить сывороточные белки. При полной коагуляции сывороточные белки в виде хлопьев поглощаются казеиновым сгустком и выход творога увеличивается. Поэтому пастеризацию проводят при 80 °С с выдержкой 20…30 с, что способствует получению достаточно плотного сгустка, хорошо отделяющего сыворотку. На стадии охлаждения молока необходимо строго соблюдать температурный режим и гигиенические требования, иначе начнут развиваться микроорганизмы, а именно термоустойчивые молочнокислые палочки незаквасочного происхождения, остающиеся в пастеризованном молоке, что вызывает повышение кислотности. А это способствует возникновению дефектов, таких как кислый вкус. Кислый вкус также возникает при перекашивании сгустка, на стадиях сквашивания и образования сгустка. На стадии заквашивания горький вкус появляется при накоплении горьких продуктов распада белков под влиянием пептонизирующих бактерий. Мажущаяся консистенция образуется в твороге, приготовленном сычужно-кислотным способом, при излишней кислотности сгустка. При излишне высокой температуре нагрева сгустка возникает сухая рассыпчатая консистенция.При удлинении сроков самопрессования и прессования творога и несвоевременном и недостаточном охлаждении наблюдается излишне кислый вкус. Несвежие, затхлые вкус, и запах возникают при нарушении санитарных условий производства, использовании плохо простиранных мешочков для самопрессования творога, а также при хранении его в плохо вентилируемых помещениях. На стадиях фасовки и хранения возможны ослизнение и плесневение творога, ослизлая консистенция. Все эти дефекты и пороки можно избежать, соблюдая правильный технологический режим производства, гигиенические требования персонала и оборудования, условия хранения. 3 Практическая часть На предприятии по производству молочной продукции ОАО «Буренкина радость» производится комплекс работ по оценке качества молочной и кисломолочной продукции, в частности, творога. При этом анализ определения жирности продукции в зависимости от различных показателей дал следующие результаты, таблица 4. Таблица 4 – Показатели жирности творога
Определить, каким образом состав основных компонентов и кислотности влияют на определение жирности творога. Решение: По данным регрессионного анализа в Excel было получено: 1. Парный коэффициент корреляции равный 0,66. Такое значение коэффициента корреляции свидетельствует о тесноте зависимости оценки жирности творога от белков, углеводов, золы и кислотности. Проверим уровень значимости полученного коэффициента путем проверки статистических гипотез. В качестве нулевой гипотезы
Парный коэффициент корреляции признается значимым, если :
То есть основная гипотеза отвергается, и принимается альтернативная. Между оценкой жирности и данными показателями существует сильная связь. 2. Но следует учитывать также, что в поставленной задаче рассматривалось лишь 44% (множественный коэффициент корреляции) величин, которые могут повлиять на оценку жирности творога, нужно искать дополнительные фактор 3. Найдем коэффициенты регрессии и проверим их значимость. Таблица 5 – Дисперсионный анализ
С помощью Excel, методом наименьших квадратов найдем коэффициенты регрессии: Таблица 6 – Регрессионный анализ
В качестве нулевой гипотезы
Оценив значимость всех коэффициентов, можно составить уравнение регрессии:
где Проанализировав полученное уравнение можно сделать вывод: Жирность творога зависит от всех данных показателей, в большей степени она связана с показателями концентрации белка и углеводов и в меньшей степени – кислотностью. Но следует учитывать также, что в поставленной задаче рассматривалось лишь 44% величин, которые могут повлиять на оценку жирности творога и поэтому уравнение не дает полной картины анализа, следовательно, нужно искать дополнительные факторы. Заключение Список использованных источников 1. Шалыгина, Е. А. Общая технология молока и молочных продуктов: учебник Е.А. Шалыгина -2-е изд. – М. : Колос, 2001. 2. Творог. – Режим доступа: URL: http://www.wikipedia.ru/ 3. Производство творога. – Режим доступа: URL: http://www.milkbranch.ru/publ/view/80.html 4. Современные техника и технология производства традиционного творога / З.Сметана, М. Холдинский, К. Сковронский // Молочная промышленность. – 2007. – №1. – С.78 – 80. 5. Технический регламент на молоко и молочную продукцию: федеральный закон № 88 от 12 июня 2008 г. Принят Государственной Думой 23 мая 2008 года. 6. Ефремов В.В. Статистические методы в управлении качества продукции / В.В. Ефремов, Т.В. Барт. – М.: КНОРУС, 2006. – 240 с. 7. Кремер Н.Ш. Теория вероятности и математическая статистика / – М.: ЮНИТА-ДАНА, 2002. – 542 с. 8. Творог. – Режим доступа: URL: http://www.ecatalog.kz. | |||||||||||||||||||

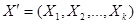 может быть представлена в следующем виде:
может быть представлена в следующем виде: 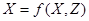 , где Z – набор случайных величин, оказывающих влияние на изучаемые случайные величины.
, где Z – набор случайных величин, оказывающих влияние на изучаемые случайные величины.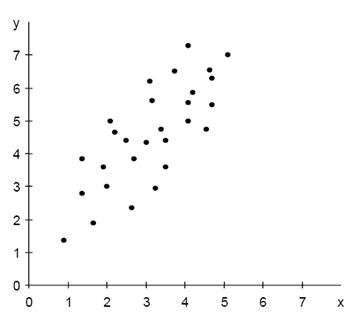
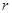 . Парный коэффициент корреляции в случае линейной формы связи вычисляют по формуле
. Парный коэффициент корреляции в случае линейной формы связи вычисляют по формуле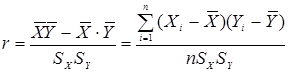 . (1)
. (1)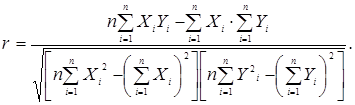 (2)
(2)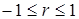 .
.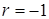 между двумя переменными существует функциональная связь, при
между двумя переменными существует функциональная связь, при 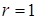 – прямая функциональная связь. Если
– прямая функциональная связь. Если 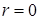 , то значение X иY в выборке некоррелированны; в случае, если система случайных величин
, то значение X иY в выборке некоррелированны; в случае, если система случайных величин 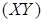 имеет двумерное нормальное распределение, то величины X иY будут и независимыми.
имеет двумерное нормальное распределение, то величины X иY будут и независимыми.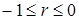 , то между величинами X иY существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины Y от среднего значения взяты с обратным знаком.
, то между величинами X иY существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины Y от среднего значения взяты с обратным знаком.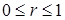 .
.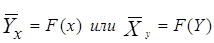 , (4)
, (4)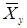 и
и 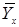 являются средними арифметическими переменных X и Y .
являются средними арифметическими переменных X и Y .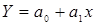 , (5)
, (5)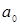 – свободный член,
– свободный член, 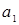 – коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.
– коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.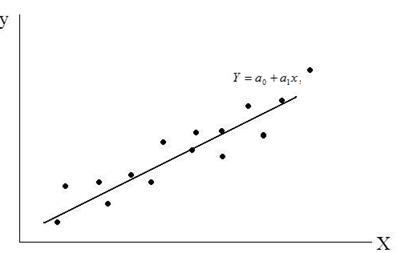
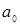 ,
, 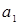
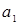 вычисляютсяпо формуле:
вычисляютсяпо формуле: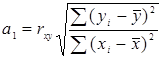 , (6)
, (6)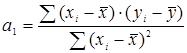 . (7)
. (7)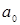 вычисляется по формуле [6]:
вычисляется по формуле [6]: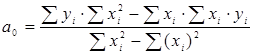 . (8)
. (8)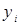 от выровненных
от выровненных 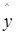 :
: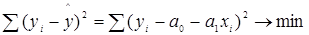 . (9)
. (9)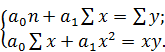 (10)
(10)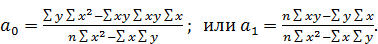 (11)
(11)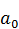
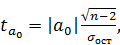 (12)
(12)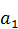
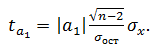 (13)
(13)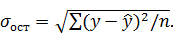 (14)
(14)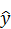 .
.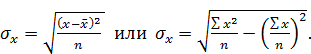 (15)
(15)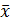 .
.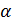 (это вероятность, с которой может быть опровергнута гипотеза о том или ином законе распределения) и числом степеней свободы вариации
(это вероятность, с которой может быть опровергнута гипотеза о том или ином законе распределения) и числом степеней свободы вариации 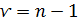 . В статистических исследованиях уровень значимости обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если
. В статистических исследованиях уровень значимости обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если 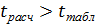 . В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.
. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.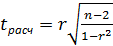 , (16)
, (16) и объеме выборки n .
и объеме выборки n .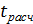 сравнивают с
сравнивают с 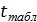 (для
(для  ). Если рассчитанное значение
). Если рассчитанное значение 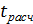 превосходит табличное значение критерия
превосходит табличное значение критерия 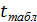 то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности) [7].
то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности) [7].
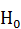 принимаем, что полученный в результате обработки данный коэффициент корреляции
принимаем, что полученный в результате обработки данный коэффициент корреляции 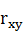 не значим, то есть корреляции между оценкой жирности и данными показателями или нет или она слабая. За альтернативную гипотезу
не значим, то есть корреляции между оценкой жирности и данными показателями или нет или она слабая. За альтернативную гипотезу 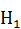 принимаем событие, что между оценкой жирности и данными показателями существует сильная связь. Проверку значимости коэффициента будем проводить по критерию согласия Стьюдента.
принимаем событие, что между оценкой жирности и данными показателями существует сильная связь. Проверку значимости коэффициента будем проводить по критерию согласия Стьюдента.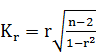 ,
, 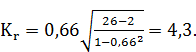
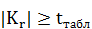 ,
,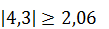
 принимаем, что полученный в результате обработки данный коэффициент не значим, то есть показатель не влияет на оценку жирности. За альтернативную гипотезу
принимаем, что полученный в результате обработки данный коэффициент не значим, то есть показатель не влияет на оценку жирности. За альтернативную гипотезу 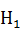 принимаем, что коэффициент регрессии значим – показатель влияет. Проверку значимости коэффициента будем проводить по критерию согласия Фишера. Если
принимаем, что коэффициент регрессии значим – показатель влияет. Проверку значимости коэффициента будем проводить по критерию согласия Фишера. Если 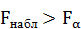 , то основная гипотеза отклоняется, коэффициент значим.
, то основная гипотеза отклоняется, коэффициент значим.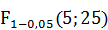 =2,6.
=2,6.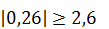 – основная гипотеза отвергается, вода влияет на оценку жирности творога;
– основная гипотеза отвергается, вода влияет на оценку жирности творога;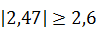 – основная гипотеза отвергается, концентрация белка влияет на оценку жирности творога;
– основная гипотеза отвергается, концентрация белка влияет на оценку жирности творога;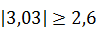 – основная гипотеза отвергается, концентрация углеводов влияет на оценку жирности творога;
– основная гипотеза отвергается, концентрация углеводов влияет на оценку жирности творога;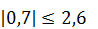 – основная гипотеза принимается, зола не влияет на оценку жирности творога;
– основная гипотеза принимается, зола не влияет на оценку жирности творога;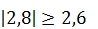 – основная гипотеза отвергается, кислотность влияет на оценку жирности творога;
– основная гипотеза отвергается, кислотность влияет на оценку жирности творога;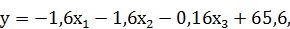
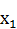 – концентрация белка,
– концентрация белка, 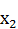 – углеводы,
– углеводы, 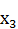 – кислотность, 65,6 – нормирующий коэффициент.
– кислотность, 65,6 – нормирующий коэффициент.