- Вид работы: Курсовая работа (т)
- Предмет: Культурология
- Язык: Русский , Формат файла: MS Word 1,52 Мб
Золотое сечение в искусстве
МИНЕСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Дальневосточный государственный гуманитарный университет»
ФАКУЛЬТЕТ ИЗОБРАЗИТЕЛЬНЫХ ИСКУССТВ И ДИЗАЙНА
КУРСОВАЯ РАБОТА
«Золотое сечение в искусстве»
Студентки 2 курса
П. А. Сорокиной
Научный руководитель
О.Т. Титова
ст. преподаватель
Хабаровск 2012
Оглавление
Введение
История развития золотого сечения
Античность
Средние века
Возрождениевек
Значение золотого сечения в искусстве
Живопись
Музыка
Архитектура
Литература
Применение золотого сечения в современном мире
Дизайн
Заключение
Использованная литература
Приложение
Введение
Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете – посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная. Садясь на скамейку, вы произвели «золотое сечение».
Цели работы это, прежде всего, изучить историю золотого сечения, изучить использование «божественной пропорции» в искусстве и познакомиться, с современны использованием золотого сечения.
О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий – свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» – это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые – от Пачоли до Эйнштейна – будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой – 1,6180339887.[2]
Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое – все подчиняется божественному закону, имя которому – «золотое сечение».
Так что же такое «золотое сечение»? Что это за идеальное, божественное сочетание? Может быть, это закон красоты? Или все-таки он – мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее – нет, известен. «Золотое сечение» – это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна.
Порой профессиональные художники, научившись рисовать и писать с натуры, по причине собственной слабой фундаментальной подготовки, считают, что знания законов красоты, (в частности закона золотого сечения) мешают свободному интуитивному творчеству. Это большое и глубокое заблуждение многих художников, так и не ставших истинными творцами. Мастера Древней Греции, умевшие сознательно пользоваться золотой пропорцией, что, в сущности, весьма просто, умело применяли ее гармонические величины во всех видах искусства и достигли такого совершенства строения форм, выражающих их общественные идеалы, какое редко встречается в практике мирового искусства. Вся античная культура прошла под знаком золотой пропорции. Знали эту пропорцию и в Древнем Египте. [10]
Знание законов золотого сечения или непрерывного деления, как его называют некоторые исследователи учения о пропорциях, помогают художнику творить осознанно и свободно. Используя закономерности золотого сечения, можно исследовать пропорциональную структуру любого художественного произведения, даже если оно создавалось на основе творческой интуиции. Эта сторона дела имеет немаловажное значение при изучении классического наследия и при искусствоведческом анализе произведений всех видов искусств.
Сейчас с уверенностью можно сказать, что золотая пропорция – это та основа формообразования, применение которой обеспечивает многообразие композиционных форм во всех видах искусства и дает основание создать научную теорию композиции и единую теорию пластических искусств.
В работе рассматриваются первые упоминания о золотом сечении, история его развития, использование в искусстве и современное виденье золотого сечения.
История развития золотого сечения
Античность
История “Золотого сечения” – это история человеческого познания мира. Понятие “Золотое сечение” прошло в своем развитии все стадии познания. Первая ступень познания открытие “золотого сечения” древними пифагорейцами. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
И действительно, пропорции пирамиды Хеопса,(1) храмов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. В начале 20-го века в Саккаре (Египет) археологи вскрыли склеп, в котором были погребены останки древне-египетского зодчего по имени Хеси-Ра. В литературе это имя часто встречается как Хесира. Предполагается, что Хеси-Ра был современником Имхотепа, жившего в период правления фараона Джосера (27-й век до н.э.) [8]
Из склепа наряду с различными материальными ценностями были извлечены деревянные доски-панели, покрытые великолепной резьбой, которую исполнила рука безупречного мастера. Всего в склепе помещалось 11 досок; из них сохранилось только пять, а остальные панели полностью разрушены Долгое время назначение панелей из захоронения Хеси-Ра было неясным.(2) Вначале египтологи приняли эти панели за ложные двери. Однако, начиная с 60-х годов 20-го века, ситуация с панелями начала проясняться. В начале 60-х годов русский архитектор И. Шевелев обратил внимание на то, что на одной из панелей жезлы, которые зодчий держит в руках, соотносятся между собой как
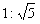
, то есть как малая сторона и диагональ с отношением сторон 1:2 ("двухсмежный квадрат"). Именно это наблюдение стало исходной точкой для исследований русского архитектора И. Шмелева, который провел тщательный геометрический анализ "панелей Хеси-Ра" и в результате пришел к сенсационному открытию, описанному в брошюре "Феномен Древнего Египта" (1993).[12]
«Но теперь, после всестороннего и аргументированного анализа методом пропорций мы получаем достаточные основания утверждать, что панели Хеси-Ра – это система правил гармонии, кодированная языком геометрии…
Итак, в наших руках конкретные вещественные доказательства, "открытым текстом" повествующие о высочайшем уровне абстрактного мышления интеллектуалов из Древнего Египта. Автор, резавший доски, с изумительной точностью, ювелирным изяществом и виртуозной изобретательностью продемонстрировал правило ЗС (золотого сечения) в его широчайшем диапазоне вариаций. В результате была рождена ЗОЛОТАЯ СИМФОНИЯ, представленная ансамблем высокохудожественных произведений, не только свидетельствующих о гениальной одаренности их создателя, но и убедительно подтверждающих, что автор был посвящен в магические таинства гармонии. Этим гением был Золотых Дел Мастер по имени Хеси-Ра".»
Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответсвуют величинам золотого деления. [12]
Вся древнегреческая культура развивалась под знаком золотой пропорции. Идея гармонии, основанной на золотом сечении, не могла не коснуться греческого искусства. Природа, взятая в широком смысле, включала в себя и творческий мир человека, искусство, музыку, где действуют те же законы ритма и гармонии. Взять материал и исключить все лишнее – таков афористически запечатленный план ваятеля, вобравшего в себя всю серьезность философской мудрости античного мыслителя. И это – главная идея греческого искусства, для которого "золотое сечение" впервые стало некоторым эстетическим каноном.
Основу искусства составляет теория пропорций. И, конечно же, вопросы пропорциональности не могли пройти мимо Пифагора. Из философов Греции Пифагор, может быть впервые, старается математически разобрать существо гармонических пропорций. Пифагор знал, что интервалы октавы могут быть выражены числами, которые отвечают соответствующим колебаниям струны, и эти числовые отношения были положены Пифагором в основу их музыкальной гармонии. Пифагору приписывают знание арифметической, геометрической и гармонической пропорций, а также закона золотого сечения. Последнему Пифагор придавал особое, выдающееся значение, сделав пентаграмму или звездчатый пятиугольник отличительным знаком своего "союза".[7]
Платон, заимствуя пифагорейское учение о гармонии, использует пять правильных многогранников ("платоновых тел") и подчеркивает их "идеальную" красоту.
Не только философы Древней Греции, но и многие греческие художники и архитекторы уделяли значительное внимание достижению пропорциональности. И это подтверждается анализом архитектурных сооружений греческих зодчих. Фригийские гробницы и античный Парфенон, "Канон" Поликлета и Афродита Книдская Праксителя, наиболее совершенный греческий театр в Эпидавре и древнейший из дошедших до нас театр Диониса в Афинах – все это яркие образцы ваяния и творчества, исполненные глубокой гармонии на основе золотого сечения.
Театр в Эпидавре построен Поликлетом Младшим в 40-ю Олимпиаду. Рассчитан на 15 тысяч человек. Театрон (место для зрителей) делится на два яруса: первый имеет 34 ряда мест, второй – 21 (числа Фибоначчи!). Раствор угла, объемлющего пространство между театроном и скеной (пристройка для переодевания актеров и хранения реквизита), делит окружность основания амфитеатра в отношении 137°,5 : 222°,5 = 0.618 (золотая пропорция). Это соотношение реализовано практически во всех античных театрах. Данная пропорция у Витрувия в его схематических изображениях такого рода построек, составляет 5:8, то есть рассматривается как отношение чисел Фибоначчи.[8]
Театр Диониса в Афинах трехъярусный. Первый ярус имеет 13 секторов, второй -21 (числа Фибоначчи!). Отношение растворов углов, делящих окружность основания на две части – то же самое, то есть золотая пропорция.
При построении храмов за основу брался человек как "мера всех вещей": в храм он должен входить "с гордо поднятой головой". Его рост делился на 6 единиц (греческих футов), которые откладывались на линейке, а на нее наносилась шкала, жестко связанная с последовательностью шести членов ряда Фибоначчи: 1, 2, 3, 5, 8, 13 (их сумма равна 32=25). Прибавлением или вычитанием этих эталонных отрезков достигались необходимые пропорции сооружения. Шестикратное увеличение всех отложенных на линейке размеров сохраняло гармоническую пропорцию. В соответствии с этой шкалой и строили храмы, театры или стадионы.
Также о золотом делении знал Платон. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.[3]
Таким образом, античность была полностью подчинена пропорции золотого сечения. В архитектуре, скульптуре, живописи и музыке прослеживалось пропорциональное деление. Гармония была присуща всей жизни.
Средние века
Одной из интереснейших личностей эпохи крестовых походов, предвестницы эпохи Возрождения, был император Фридрих Гогенштауфен, ученик сицилийских арабов и поклонник арабской культуры. При его дворце в Пизе жил и работал величайший из европейских математиков средних веков Леонардо Пизано (по прозвищу Фибоначчи)
Фибоначчи написал несколько математических сочинений: "Liber abaci", "Liber quadratorum", "Practica geometriae". Наиболее известным из них является "Liber abaci". Это сочинение вышло при жизни Фибоначчи в двух изданиях в 1202 г. и 1228 г. Книга состоит из 15 разделов. Заметим, что Фибоначчи задумывал свое сочинение как пособие для купцов, однако по своему значению оно вышло далеко за пределы торговой практики и по существу представляло своеобразную математическую энциклопедию эпохи средневековья. С этой точки зрения особенный интерес представляет 12-й раздел, в котором Фибоначчи (3) сформулировал и решил ряд математических задач, представляющих интерес с точки зрения общих перспектив развития математики. [2]
Наиболее известной из сформулированных Фибоначчи задач является рассмотренная выше "задача о размножении кроликов", которая привела к открытию числовой последовательности 1, 1, 2, 3, 5, 8, 13, …, названной впоследствии "рядом Фибоначчи".
Фибоначчи почти на два столетия опередил западно-европейских математиков своего времени. Подобно Пифагору, который получил свое "научное образование" у египетских и вавилонских жрецов и затем способствовал передаче полученных знаний в греческую науку, Фибоначчи получил свое математическое образование в арабских учебных заведениях и многие из полученных там знаний, в частности, арабо-индусскую десятичную систему счисления, он попытался "внедрить" в западно-европейскую науку. И подобно Пифагору историческая роль Фибоначчи для западного мира состояла в том, что он своими математическими книгами способствовал передаче математических знаний арабов в западно-европейскую науку и тем самым заложил основы для дальнейшего развития западно-европейской математики.[11]
Итак, средневековье узнало о золотой пропорции в математическом варианте (в виде последовательности чисел Фибоначчи). Сохранение знаний о «божественной пропорции» послужило основой для дальнейшего развития искусства уже эпохи Возрождения.
Возрождение
Ренессанс в истории культуры стран Западной и Центральной Европы – переходная эпоха от средневековой культуры к культуре нового времени. Наиболее характерной чертой этой эпохи является гуманистическое мировоззрение и обращение к античному культурному наследию, как бы "возрождение" античной культуры. Эпоха Возрождения отмечена крупными научными сдвигами в области естествознания. Специфической особенностью науки этой эпохи была тесная связь с искусством, и это объединение иногда выражалось в творчестве одной личности. Наиболее ярким примером такой многогранной личности является Леонардо да Винчи – художник, ученый, инженер.[13]
Вместе с другими достижениями античной культуры ученые и художники эпохи Возрождения с огромным энтузиазмом восприняли пифагорейскую идею гармонии Мироздания и золотое сечение. И не случайно, что именно Леонардо да Винчи, который является одной из наиболее ярких личностей эпохи Возрождения, вводит в широкое употребление название "золотое сечение", которое сразу же становится эстетическим каноном эпохи Возрождения.
Идея гармонии оказалась в ряду тех концептуальных построений античной культуры, к которым церковь отнеслась с большой заинтересованностью. Согласно христианской доктрине Веленная была творением Бога и беспрекословно подчинялась его воле. И христианский Бог при сотворении мира руководствовался математическими принципами. Эта католическая доктрина в науке и искусстве Возрождения приобрела форму поиска математического плана, по которому Бог создал Вселенную.
Убеждение в том, что природа сотворена по математическому плану и что творцом гармонии является Господь Бог, выражали в тот период не только ученые, но и поэты, а также представители искусства.[3]
По мнению современного американского историка математики Мориса Клайна именно тесное слияние религиозной доктрины о Боге как творце Вселенной и античной идеи о числовой гармонии Мироздания, стало одной из важнейших причин огромного всплеска культуры в эпоху Возрождения. Наиболее ярко главная цель науки эпохи Возрождения изложена в следующем высказывании Иоганна Кеплера:
"Главной целью всех исследований внешнего мира должно быть открытие рационального порядка и гармонии, которые Бог ниспослал миру и открыл нам на языке математики".[12]
Эта же идея, идея гармонии мира, выражение его упорядоченности и совершенства, превращается в главную идею искусства эпохи Возрождения. В произведениях Браманте, Леонардо да Винчи, Рафаэля, Джордано, Тициана, Альберти, Донателло, Микеланджело проявляется строгая соразмерность и гармоничность сюжета, подчиняющаяся выверенной пропорции. Наиболее выпукло закон гармонии, закон числа, с которым связывалась красота произведения, раскрывался в художественных произведениях и научно-методических исследованиях Леонардо, Дюрера, Альберти.
В период эпохи Итальянского Возрождения продолжаются исследования в области теории пропорциональности произведений скульптуры и архитектуры. В этот период в Италии переиздаются сочинения знаменитого римского архитектора Витрувия, оказавшие определяющее влияние на труды итальянских теоретиков искусства (Альберти). Возникнув во Флоренции, классический стиль Высокого Возрождения создал свои наиболее монументальные памятники в Риме, Венеции и других культурных центрах Италии.
Помимо художников, архитекторов и скульпторов этой эпохи под сильным влиянием античных идей о гармонии оказалась вся музыкальная культура. В этот период известный философ, физик и математик М. Мерсенн вводит в музыку 12-звуковой темперированный строй. В ряде свих работ – "Трактат о всеобщей гармонии", "Всеобщая гармония" Мерсенн рассматривает музыку как неотъемлемую часть математики и видит в ней – в ее консонансном звучании – один из основных способов проявления мировой гармонии и красоты.
Именно в этот период появляется первая книга, посвященная "золотому сечению". [10]
XIX век
В 19 в. коренным образом меняется характер науки. Проблема структурного единства мира, выдвинутая еще в античности, постепенно возрождается в своем гносеологическом статусе, обеспечивается всем достоянием науки. Идея структурного единства мира подтверждается эволюционным учением в биологии (Ч. Дарвин), внесшим в естествознание идею развития, периодическим законом (Д.И. Менделеев), позволившем прогнозировать свойства еще неизвестных химических элементов, законом сохранения и превращения энергии (Р. Майер, Дж. Джоуль, Г. Гельмгольц), поставившем на единую основу все законы физики и химии,клеточной теорией (Т. Шванн, М. Шлейден), показавшей единообразную структуру всех живых организмов, и другими выдающимися научными открытиями науки 19-го века, доказавшими наличие внутренней связи между всеми известными видами вещества.
Последовательно проведенный в античности тезис о единстве человека и природы вновь возрождается на исходе 19-го и главным образом в первой половине 20-го века в ряде концептуальных построений, особенно в рамках так называемого "русского космизма" (В.И Вернадский, Н.Ф. Федоров, К.Э. Циолковский, П.А. Флоренский, А.Л. Чижевский и др.). Важнейшим направлением исследований становится поиск инвариантов бытия – особых устойчивостей, обнаруживающихся в целых классах внешне различных или разнородных явлений, способных вскрывать и выражать общую природу последних.[8]
В 19-м веке большой вклад в развитие теории пропорциональности внес немецкий ученый А. Цейзинг, (4) книга которого "Neue Lehre von den Prportionen des menschlichen Korpers" (1854) является до сих пор широко цитируемой среди сочинений, посвященных проблеме пропорциональности.
Исходя из того положения, что пропорциональность есть отношение двух неравных частей между собой и к целому в наиболее совершенном их сочетании, Цейзинг формулирует закон пропорциональности следующим образом:
"Деление целого на неравные части пропорционально, когда отношение частей целого между собой то же, что и отношение их к целому, т.е. то отношение, которое дает золотое сечение".
Пытаясь доказать, что все мироздание подчиняется этому закону, Цейзинг старается проследить его как в органическом, так и в неорганическом мире.
В подтверждение этого он приводит данные об отношениях взаимных расстояний между собой небесных светил, отвечающих золотому сечению, устанавливает такие же отношения в строении человеческой фигуры, в конфигурации минералов, растений, в звуковых аккордах музыки в архитектурных произведениях.
Рассмотрев статуи Аполлона Бельведерского и Венеры Медицейской, Цейзинг устанавливает, что при делении общей высоты в указанном отношении линии деления проходят через естественные членения тела. Первый раздел проходит через пупок, второй через середину шеи т.д., то есть все размеры отдельных частей тела получаются путем деления целого по золотому сечению.
Останавливаясь на значении закона золотого сечения в музыке, Цейзинг указывает, что древние греки приписывали эстетическое впечатление аккордов пропорциональному делению октавы при помощи среднеарифметической и гармонической пропорции. Первой отвечает отношение основного тона к квинте и к октаве – 6:9:12; второй – отношение основного тона к кварте и к октаве – 6:8:12. Таким же образом греки объяснили гармонию и остальных созвучий.[9]
Базируясь на тех положениях, что только те соединения тонов красивы, интервалы которых находятся между собой и к целому в пропорциональном отношении, и на том, что соединение только двух тонов не дает полной гармонии, Цейзинг показывает, что наиболее приятные для слуха консонансы имеют такие интервалы, что соотношение частот, входящих в аккорд, в наибольшей степени близко к золотой пропорции. Например, соединению малой терции с октавой основного звука соответствует отношение частот 3:5, соединение большой терции с октавой основного звука – 5:8 (3, 5, 8 – числа Фибоначчи!).
Далее Цейзинг делает вывод, что так как эти два соединения звуков между двузначными самые приятные для слуха, то этим, по-видимому, объясняется тот факт, что только ими заканчиваются музыкальные периоды. Этим же он объясняет, почему импровизированный народный напев и простая музыка двух валторн (или английских рожков) движется в секстах и их дополнениях – терциях.
Цейзинг обращает внимание еще на один любопытный факт. Как известно, мажорный (мужской) и минорный (женский) лады построены на основе мажорного и минорного трезвучия. Мажорное трезвучие, построенное на основе большой терции, является консонансом акустически правильным. Оно создает впечатление уравновешенности, физического совершенства, придающего ему характер силы, света, бодрости, объединяемых в жизни понятием "мажорности".
Минорное трезвучие, построенное на основе малой терции, является консонансом акустически неправильным. Оно создает впечатление сломленного звучания и имеет характер мрачности, печали, слабости, объединяемых в жизни понятием "минорности".
Эти выводы Цейзинга с его толкованием причин консонансности интервалов подтверждаются исследованиями акустиков.
Переходя к значению закона пропорциональности в архитектуре, Цейзинг указывает, что архитектура в области искусств занимает такое же положение, как и органический мир в природе, одухотворяя на почве мировых законов инертную материю. Планомерность, симметрия и пропорциональность при этом являются непременными ее атрибутами, откуда вытекает, что вопрос о законах пропорциональности в архитектуре стоит значительно острее, чем в скульптуре или в живописи.[7]
Таким образом, наука 19-го столетия опять возвратилась к поиску ответа на те "вечные" вопросы, которые были поставлены еще древними греками. Созрело убеждение, что в мире господствует "универсальный закон" числа и ритма, выражающие его структурную и функциональную стороны. В этой связи в науке 19-го века вновь пробуждается интерес к золотому сечению.
Значение золотого сечения в искусстве
Итак, прежде чем определить золотое сечение, необходимо ознакомиться с понятием пропорции. В математике пропорция (лат. proportio) – это равенство между двумя отношениями четырех величин: а : Ь = с : d. Далее, для примера обратимся к отрезку прямой. Отрезок АВ можно разделить на две равные части (/). Это будет соотношение равных величин – АВ : АС = АВ : ВС. Эту же прямую (5) можно разделить на две неравные части в любом отношении. Эти части пропорции не образуют. Отношение малого отрезка к большому или меньшего к большему есть, а соотношения (пропорции) нет. И, наконец, прямую АВ можно разделить по золотому сечению, когда АВ : АС, как АС : ВС. Это и есть золотое деление или деление в крайнем и среднем отношении. Из вышеизложенного следует вывод, что золотое сечение – это такое пропорциональное гармоническое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему, т. е. a: b = b : с или с Ь = b : а. Определение – деление в крайнем и среднем отношении – становится более понятным, если мы выразим его геометрически , а именно а : b как b : с.
Выводим золотую пропорцию. (6) Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка f делит отрезок АВ в соотношении золотой пропорции. Арифметически отрезки золотой пропорции выражаются бесконечной иррациональной дробью. АЕ = 0,618…, если АВ принять за единицу, ff = 0,382…. В практике применяется округление: 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.[13]
Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.(7)
Форма спирально завитой раковины привлекла внимание еще древнегреческого ученого Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спиралью Архимеда. Увеличение ее шага всегда равномерно.
Так где же мы сможем встретить золотое сечение в искусстве.
Живопись
Очень часто в одном и том же произведении живописи встречается сочетание симметричного деления на равные части по вертикали и деление на неравные части по золотому сечению по горизонталям. Рассмотрим примеры.
В знаменитом портрете Монны Лизы ("Джоконды")(8), который был завершен Леонардо да Винчи в 1503 г., важным элементом композиции становится космически обширный пейзаж, таящий в холодной дымке. Картина гениального художника привлекла внимание исследователей, которые обнаружили, что композиционное построение картины основано на двух "золотых" треугольниках, которые являются частями "пентаграммы".
Картина Леонардо да Винчи «Мадонна в гроте» (9) не строго симметрична, но в основе ее построения – симметрия. Все содержание картины выражается в фигурах, которые разместились в нижней ее части. Они вписываются в квадрат. Но художник не довольствовался таким форматом. Он достраивает над квадратом прямоугольник золотого сечения. В результате такого построения вся картина получила формат золотого прямоугольника, поставленного вертикально. Радиусом, равным половине стороны квадрата, он описал окружность и получил полукружие верхней части картины. Внизу дуга пересекла ось симметрии и указала размер еще одного прямоугольника золотого сечения в нижней части картины. Затем радиусом, равным стороне квадрата, описывается новая дуга, которая дала точки на вертикальных сторонах картины. Эти точки помогли построить равносторонний треугольник, который и явился каркасом для построения всей группы фигур. Все пропорции в картине явились производными от высоты картины. Они образуют ряд отношений золотого сечения и служат основой гармонии форм и ритма, несущих в себе скрытый заряд эмоционального воздействия.[12]
Аналогичным образом построена картина Рафаэля «Обручение Марии».
Широкое использование "золотой" спирали характерно для художественных произведений Рафаэля, Микеланджело и других итальянских художников.
Многофигурная композиция "Избиение младенцев" (10), выполненная в 1509-1510 годах Рафаэлем, отличается динамизмом и драматизмом сюжета. На подготовительном эскизе Рафаэля проведена плавная линия, охватывающая всю картину. Линия начинается в смысловом центре композиции – точке, где пальцы воина сомкнулись вокруг лодыжки ребенка, и далее идет вдоль фигуры ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить все эти куски кривой пунктиром, то с очень высокой точностью получается "золотая" спираль!
Фигура А. С. Пушкина в картине Н. Н. Ге «Александр Сергеевич Пушкин в селе Михайловском» (11) поставлена художником на линии золотого сечения в левой части полотна. Но и все остальные величины по ширине вовсе не случайны: ширина печи равна 24 частям от ширины картины, этажерки – 14 частям, расстояние от этажерки до печи также равно 14 частям и т. д.[1]
Если мы обратимся к древнерусской живописи, иконам XV – XVI вв., то увидим такие же приемы построения изображения. Иконы вертикального формата симметричны по вертикали, а членения по горизонталям осуществлены по золотому сечению. Икона «Сошествие во ад» Дионисия и мастерской с математической точностью рассчитана в пропорциях золотого сечения.
В иконе конца XV в. «Чудо о Флоре и Лавре» осуществлено тройное отношение золотого сечения. Сначала мастер разделил высоту иконы на две равные части. Верхнюю отвел под изображение ангела и святых. Нижнюю часть он разделил на два неравных отрезка в отношении 3 : 2. В итоге получилось соотношение трех величин золотого сечения: а:b, как b:с. В числах это будет выглядеть так: 100, 62, 38, а уменьшенные вдвое – 50, 31, 19.
О симметричности «Троицы» (12) Андрея Рублева написано много. Но никто не обратил внимания на то, что по горизонталям и здесь осуществлен принцип золотых пропорций. Высота среднего ангела относится к высоте боковых ангелов, как их высота относится к высоте всей иконы. Линия золотого сечения пересекает ось симметрии по середине стола и чаши с жертвенным тельцем. Это – композиционный замок иконы. На рисунке показаны и более мелкие величины ряда золотого сечения. Наряду с плавностью линий, колоритом пропорции иконы играют значительную роль в создании того общего впечатления, которое испытывает зритель при ее рассматривании.[13]
Могучим хоралом представляется нашему взору икона Феофана Грека «Успение». Симметрия и золотое сечение в построении придают этой иконе такую мощь и стройность, какую мы видим и ощущаем при виде греческих храмов и слушании фуг Баха. Легко заметить, что композиция «Успения» Феофана Грека и «Троицы» Андрея Рублева одна и та же. Исследователи творчества древнерусских художников отмечают, что заслуга Феофана Грека состоит не столько в том, что он писал фрески и иконы для русских соборов и церквей, сколько в том, что он научил античной мудрости Андрея Рублева.
Музыка
Музыка – вид искусства, который отражает действительность и воздействует на человека посредством осмысленных и особым образом организованных звуковых последовательностей, состоящих из тонов. Сохраняя некоторое подобие звуков реальной жизни, музыкальные звучания принципиально отличаются от последних строгой высотной и временной (ритмической) организованностью ("музыкальная гармония"). Начиная с античного периода, выяснение законов "музыкальной гармонии" является одним из важных направлений научных исследований.[5]
Пифагору приписывают установление двух основных законов гармонии в музыке:
) если отношение частот колебаний двух звуков описывается малыми числами, то они дают гармоническое звучание;
) чтобы получить гармоническое трезвучие, нужно к аккорду из двух консонансных звуков добавить третий звук, частота колебаний которого находится в гармонической пропорциональной связи с двумя первыми. Значение работ Пифагора по научному объяснению основ музыкальной гармонии трудно переоценить. Это была первая научно обоснованная теория музыкальной гармонии.
Любое музыкальное произведение имеет временное протяжение и делится некоторыми вехами ("эстетическими вехами") на отдельные части, которые обращают на себя внимание и облегчают восприятие целого. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Существуют ли какие-либо закономерности возникновения "эстетических вех" в музыкальном произведении? Попытка ответить на этот вопрос была предпринята русским композитором Л.Сабанеевым. В большой статье "Этюды Шопена в освещении золотого сечения" (1925 г.) он показывает, что отдельные временные интервалы музыкального произведения, соединяемые "кульминационным событием", как правило, находятся в соотношении золотого сечения. Сабанеев пишет:
"Все такие события инстинктом автора приурочиваются к таким пунктам длины целого, что они собою делят временные протяжения на отдельные части, находящиеся в отношениях "золотого сечения". Как показывают наблюдения, приурочение подобных эстетических "вех" к пунктам деления общего или частичного протяжения в "золотом" отношении выполняется нередко с огромной точностью, что тем более удивительно, что при отсутствии у поэтов и у авторов музыки всякого знания о подобных вещах, это все является исключительно следствием внутреннего чувства стройности".[9]
Анализ огромного числа музыкальных произведений позволил Сабанееву сделать вывод о том, что организация музыкального произведения построена так, что его кардинальные части, разделенные вехами, образуют ряды золотого сечения. Такая организация произведения соответствует наиболее экономному восприятию массы отношений и поэтому производит впечатление наивысшей "стройности" формы. По мнению Сабанеева, количество и частота использования золотого сечения в музыкальной композиции зависит от "ранга композитора". Наиболее высокий процент совпадений отмечается у гениальных композиторов, то есть "интуиция формы и стройности, как это и следует ожидать, наиболее сильна у гениев первого класса".
По наблюдениям Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, сопряженное с происходящим возле него "эстетическим событием", а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений; количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Большое внимание исследованию законов музыкальной гармонии уделял известный русский искусствовед Э.К. Розенов. Он утверждал, что в музыкальных произведениях и поэзии существуют строгие пропорциональные отношения:
"Явные черты "природного творчества" мы должны признать в тех случаях, когда в сильно одухотворенных созданиях гениальных авторов, порожденных мощным стремлением духа к правде и красоте, мы совершенно неожиданно обнаруживаем какую-то неподдающуюся непосредственному сознанию таинственную закономерность числовых отношений".
Э. Розенов считал, что золотое сечение должно играть в музыке выдающуюся роль как средство для приведения однородных явлений в соответствие, созданное самой природой:
"Золотое деление могло бы:
) устанавливать в музыкальном произведении изящное, соразмерное отношение между целым и его частями;
) являться специальным местом подготовленного ожидания, совмещаясь с кульминационными пунктами (силы, массы, движения звуков) и с разного рода выдающимися, с точки зрения автора, эффектами;
) направлять внимание слушателя на те мысли музыкального произведения, которым автор придает наиболее важное значение, которые желает поставить в связь и соответствие между собой".
Розенов выбирает для анализа ряд типичных произведений выдающихся композиторов: Баха, Бетховена, Шопена, Вагнера. Например, исследуя Хроматическую фантазию и фугу Баха, за единицу меры во времени была принята длительность четверти. В этом произведении содержится 330 таких единиц меры. Золотое деление этого интервала приходится на 204-ю четверть от начала. [4]
Э. Розеновым подробно были разобраны: финал сонаты cis-moll Бетховена, Fantasia-Impromtu Шопена, вступление к "Тристану и Изольде" Вагнера. Во всех этих произведениях золотое сечение встречается очень часто. Особое внимание автор обращает на фантазию Шопена, которая была создана экспромтом и не подлежала никакой правке, а значит и не было сознательного применения закона золотого сечения, которое присутствует в этом музыкальном произведении вплоть до мелких музыкальных образований.
Итак, можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения.
Архитектура
В архитектуре также можно наблюдать принцип золотого сечения. Например церковь Покрова на Нерли (1165 г.) (13) считается наиболее совершенным творением владимирских зодчих.
Знакомство с храмом Нерли создает образ гармонии, архитектурной красоты. И невольно возникает вопрос: какими "секретами" владели русские зодчие, творившие восемь веков назад?
Изучая архитектуру церкви Покрова на Нерли, русский архитектор И. Шевелев пришел к выводу, что в этом шедевре архитектуры проявляется пропорция
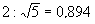
, которая представляет собой отношение большей стороны к диагонали "двухсмежного квадрата", то есть прямоугольника с отношением сторон 1:2. Таким образом, в основе взаимосвязанных пропорций этого архитектурного сооружения положены пропорции "двухсмежного" квадрата и его производная – золотая пропорция. Наличие этих пропорций и определило красоту храма. "Поразительная красота и гармоничность архитектуры храма Покрова Богородицы на Нерли, – пишет теоретик архитектуры К.Н. Афанасьев, – оформляется цепью взаимосвязанных отношений "золотого сечения".[11]
Другой пример -это собора Василия Блаженного на Красной площади Москвы. (14) История создания этого храма такова. 2 октября 1552 года пала Казань, навсегда избавив Россию от татарского нашествия. Для прославления "казанского взятия", вошедшего в историю России наравне с Куликовской битвой, царь Иван Грозный принял решение заложить на Красной площади Москвы собор Покрова; позже этот храм был прозван в народе "Василием Блаженным" в честь юродивого, который был погребен у стен храма в 16-м веке.
Для композиции построек собора характерно гармоническое сочетание симметричных и асимметричных пропорций. Храм, симметричный в своей основе, содержит много геометрических "неправильностей". Так, центральный объем шатра смещен на 3 м к западу от геометрического центра всей композиции. Однако неточность делает композицию более живописной, "живой" и она выигрывает в целом. Для архитектурного убранства собора характерно нарастание декоративных форм ввысь; формы вырастают одна из другой, тянутся вверх, подымаясь то крупными элементами, то образуя группы, состоящие из более мелких декоративных частей.
В соответствии с этой композиционной идеей построены и пропорции собора. Исследователи обнаружили в нем пропорцию, основанную на ряде золотого сечения:
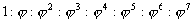
где j = 0,618. В этом членении и заключена основная архитектурная идея создания собора, единая для всех куполов, объединяющая их в одну соразмерную композицию.
При рассмотрении храма Василия Блаженного невольно возникает вопрос: случайно ли число куполов в нем равно 8 (вокруг центрального собора)? Существовали ли какие-либо каноны, определяющие число куполов в храме? Очевидно, существовали. Простейшие православные соборы раннего периода были одноглавые. После реформы патриарха Никона в середине 17-го века было запрещено строить одноглавые церкви как не соответствующие пятиглавому чину православной церкви.[11]
Помимо одно- и двухкупольных православных церквей, многие имели по 5 и 8 куполов. Однако новгородский Софийский собор (10-й век) был 13-главым, а Преображенская церковь в Кижах, вырубленную из дерева 2,5 столетия назад, венчает 21 глава. Случаен ли такой рост числа куполов "по Фибоначчи" (1, 2, 3, 5, 8, 13, 21), отражающий естественный закон роста – от простого к сложному?
Выражение "архитектура – это застывшая музыка" стало крылатым. Оно не является результатом строгого научного анализа, это скорее всего итог образного, интуитивного ощущения некой связи гармонической архитектурной формы с музыкальной гармонией. Музыкальная мелодия основана на чередовании звуков различной высоты и продолжительности, в ее основе – временная упорядоченность звуков. В основе архитектурной композиции – пространственная упорядоченность форм. Казалось бы между ними ничего общего. Но чтобы оценить размеры пространственной конструкции геометрической фигуры, мы должны проследить взглядом от начала до конца эту фигуру, и чем больше, например, длина ее, тем длительнее будет восприятие. Очевидно, здесь и заключена органическая связь пространственного и временного восприятия объектов человеком.
Литература
Представляет несомненный интерес анализ романа "Евгений Онегин", сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!
Н Васютинский констатирует:
"Кульминацией главы является объяснение Евгения в любви к Татьяне – строка "Бледнеть и гаснуть … вот блаженство!". Эта строка делит всю восьмую главу на две части – в первой 477 строк, а во второй – 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!".
Многое в структуре поэтических произведений роднит этот вид искусства с музыкой. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Каждый стих обладает своей музыкальной формой – своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных произведений, закономерности музыкальной гармонии, а следовательно, и золотая пропорция. Знаменитое стихотворение Лермонтова "Бородино" делится на две части: вступление, обращенное к рассказчику и занимающее лишь одну строфу ("Скажите, дядя, ведь недаром …"), и главную часть, представляющее самостоятельное целое, которое распадается на две равносильные части. В первой из них описывается с нарастающим напряжением ожидание боя, во второй – сам с постепенным снижением напряжения к концу стихотворения. Граница между этими частями является кульминационной точкой произведения и приходится как раз на точку деления его золотым сечением.[5]
Главная часть стихотворения состоит из 13 семистиший, то есть из 91 строки. Разделив ее золотым сечением (91:1,618 = 56,238), убеждаемся, что точка деления находится в начале 57-го стиха, где стоит короткая фраза: "Ну ж был денек!". Именно эта фраза представляет собой "кульминационный пункт возбужденного ожидания", завершающей первую часть стихотворения (ожидание боя) и открывающий вторую его часть (описание боя).[4]
Таким образом, золотое сечение играет в поэзии весьма осмысленную роль, выделяя кульминационный пункт стихотворения.
Применение золотого сечения в современном мире
В сегодняшний век высоких технологий, человек нуждается в созерцании гармонии даже в обыденных вещах. Дизайнер применяют принцип золотого сечения практически во всем от создания логотипа до дизайна автомобиля.
Дизайн
золотой сечение живопись музыка
В дизайне чаще всего и применяют ряд Фибоначчи для вычисления идеальных пропорций. Но прогресс не стоит на месте, и сегодня появились специальные чрезвычайно удобные программы, позволяющие с легкостью вычислять золотое сечение. Вам нужно лишь задать число и получить соответствующее значение.
Возможно, вы немного удивлены и не можете понять, зачем применяется золотое сечение в дизайне? Ответ можно проиллюстрировать так. Отношение сторон у iPod Shuffle 1.59, iPod Classic 1.67 , а у iPhone4 1.7 – объем продаж за первые 4 дня торговли превысил 1 миллион 700 тысяч штук. Эти результаты продаж не удивляют поклонников продукции Apple, естественно прибор оценивают по другим характеристикам. Но, мне кажется, Джонатан Айв не случайно остановился на таких пропорциях. Как не случайно уже 200 лет компания Moleskine продает по всему миру записные книжки. В книжках Moleskine оставляли записи и делали зарисовки Матисс, Ван Гог, Хемингуэй и многие другие. Это реальная история человечества в книжках с пропорциями 1.57
Золотое сечение встречается в предметном мире и в прямом прочтении, как тема для стилизации, и в качестве базового конструктивного принципа, как скрипка великого мастера Страдивари.[13]
В веб-дизайне правило золотого сечения помогает выполнять такие задачи:
) Определять, какого размера должна быть картинка и все элементы на странице.
) Владея методом золотого сечения, веб-дизайнер с легкостью может определять центры внимания на странице – т.е. именно те точки, куда направлены взгляды всех посетителей. Достаточно поместить туда нужную иллюстрацию или текст – и он попадет в поле зрения потенциальных клиентов.
Твиттер во время редизайна 2011 года использовал принцип золотого сечения в новом интерфейсе. (15) Но он сохраняет соотношение элементов сайта только в стандартной, узкой версии, если же окно будет больше, то контент растягивается.
Сайт It’s Numbered применяет принцип золотого сечения не ко всему интерефейсу, а только к связке контент+изображение.(16)
А сайт MmDesign использует золотое сечение для отображения основного визуала на главной странице.[13]
Использование золотого сечения не гарантирует, что дизайн сайта будет хорошим, есть целый ряд других, не менее важных факторов, которые способствуют разработке правильного дизайна. Однако золотое сечение может помочь придать баланс и законченность работе, а также легкость восприятия интерфейса пользователями, чего зачастую не очень просто добиться.
Использование правила золотого сечения помогает находить баланс и оптимальное сочетание в расположении различных элементов на странице.
Таким образом золотое сечение применяется в создании логотипов, в промышленном дизайне, в создании интернет ресурсов.
Заключение
золотой сечение живопись музыка
Итак, мы делаем вывод, что среди бесчисленного разнообразия форм в природе, с которыми встречается художник, царит закономерность и системность, связующей нитью которых является пропорция золотого сечения. Все существующее в природе и воспринимаемое глазом человека имеет величину и форму. Всякий природный объект является чем-то единым, целостным. Нетрудно заметить, что природа всегда создает что-то целое: человека, дерево, рыбу, лошадь, собаку и т. д. От этого целого нельзя ничего отнять, убавить, не нарушив целостность. Нельзя ничего и прибавить. Оно будет лишним и тоже нарушит целостность и гармонию. Например, шесть пальцев на руке человека, три рога у быка.[6]
В 20-м веке выполнено огромное количество искусствоведческих работ, показывающих широкое проявление и использование "золотого сечения" во всех сферах искусства: в музыке (Сабанеев "Этюды Шопена в освещении Золотого Сечения), в поэзии (академик Церетели "Золотое Сечение в поэме Шота Руставели "Витязь в тигровой шкуре"), киноискусстве (кинорежиссер Эйнштейн), архитектуре (Гримм Г.Д. "Пропорциональность в архитектуре), живописи (Ковалев Ф.В.), архитектуре (Шевелев И.Ш.), музыке (Марутаев М.А.). Большой интерес представляют исследования российского филолога Гринбаума О.Н. по выявлению "фибоначчиевых" закономерностей в поэзии А.С. Пушкина и российского философа Волошинова А.В. по исследованию математических начал формообразования в музыке, архитектуре, живописи и литературе.
Целое всегда состоит из частей. Части разной величины находятся в определенном отношении друг к другу и к целому. Это и есть пропорции. С математической точки зрения мы отмечаем повторение измеримых равных величин и неравных, соотносящихся друг с другом как величины золотой пропорции. Это – два вида пропорциональных отношений. Все другие величины, если они возникли в результате нарушения формообразования по каким-либо причинам, пропорции не составляют. Пропорциональные отношения ведут к симметрии, ритму, к гармонии и красоте. Непропорциональные отношения ведут к нарушению порядка, нарушению симметрии и ритма, что воспринимается человеком как некрасивое и даже уродливое.
Итак, природный закон божественной пропорции, проявляющийся в высших формах произведений искусства, обнаруживается в новой, ритмодинамической форме эстетического закона. Закон "золотого сечения", известный со времен Древнего Египта, является одним из самых удивительных математических законов; он был сформулирован великим Леонардо и все чаще фигурирует в стремительно нарастающем потоке естественнонаучных и гуманитарных исследований.
Этот закон не является законом принудительным, единственным или исключительным, обуславливающим художественное впечатление; тем не менее, он остается законом, непосредственно связанным с эстетическим, художественным воздействием, оказывает непосредственное влияние на впечатление цельности и красоты. Чуткий к красоте Пушкин одним только художественным инстинктом, во-первых, угадывал моменты "золотого сечения" в развитии своего повествования с поразительной по своей математической точности интуицией; во-вторых, устанавливал пропорциональные размеры частей по отношению к целому и, в-третьих, подчеркивал кульминационные пункты нарастающего по напряжению ожидания, композиционно помещая основные мысли повествования на места, столь заметные для непосредственного чувственного восприятия.
Использованная литература
1. Бендукидзе, А. Б. Золотое сечение: учебное пособие / А. Б. Бендукидзе; М, 1973. – 53-55с.
. Васютинский Н. А. Золотая пропорция: учебное пособие / Н. А. Васютинский; М: Молодая гвардия, 1990. – 238c.
3. Гика М. Эстетика пропорций в природе и искусстве: учебное пособие / М. Гика; М, 1936. – 301с.
4. Гринбаум О.Н. Гармония строфического ритма в эстетико-формальном измерении: на материале "Онегинской строфы" и русского сонета. / О.Н. Гринбаум; СПб, Изд-во СПбГУ, 2000.- 160 с. 5. Гринбаум О.Н. Русский сонет и "золотая пропорция" ритма: учебное пособие. /О. Н. Гринбаум, Г. Я. Мартыненко; СПб, Изд-во СПбГУ, 1999.- 20 с. 6. Дюрер А. Дневники, письма, трактаты: монография. /А. Дюрер; М, 1957. – Т. 2.- 37-40с, 7. Коробко В.И. Золотая пропорция и проблемы гармонии систем: учебное пособие. / В. И. Коробко; Москва, Изд-во Ассоциации строительных вузов, 1998.-1-2с. 8. Коробко В.И. Золотая пропорция и человек: учебное пособие. / В. И. Коробко Г. Н. Примак; Ставрополь, Изд-во "Кавказская библиотека", 1992.-3с. 9. Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы: учебное пособие / Л. Л. Сабанеев; Искусство, 1925. 132-145с. 10. Сороко Э.М. Структурная гармония систем: учебное пособие./ Э. М. Сороко; Минск, "Наука и техника", 1984. – 5с. 11. Стахов А.П. Коды золотой пропорции: учебное пособие./ А П. Стахов; Москва, Изд-во "Радио и Связь", 1984. – 2-4с. 12. Шмигевский Н. В. Формула совершенства /Н. В. Шмигевский; Страна знаний, 2010. -2-7с.
Приложение

. Пирамида Хеопса 2470 года до н. э
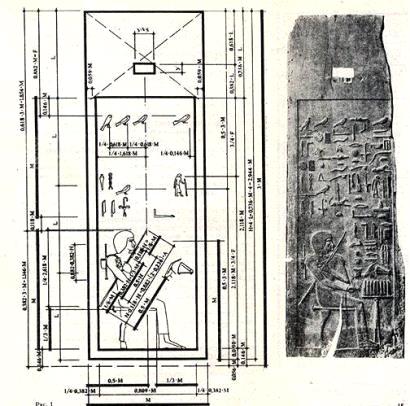
. Панель из захоронения Хеси-Ра. 27 век до н. э.


. Леонардо Пизанский (Фиббоначи) 4. Адольф Цейзинг(1810-1873) 1170-1250
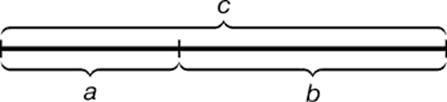
. Золотое сечение.
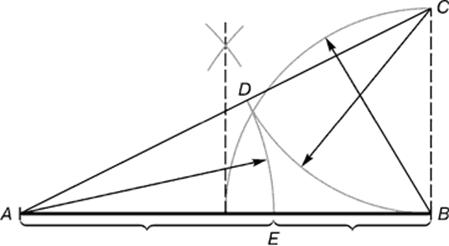
. Построение золотого сечения.
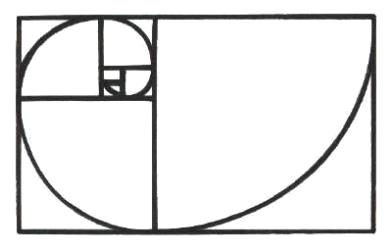
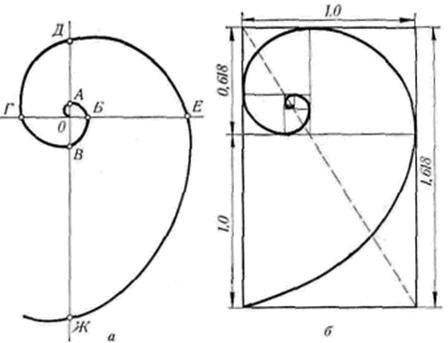
. Спирали.


. Леонардо да Винчи. 9. Леонардо да Винчи «Мадонна в гроте» «Мона Лиза» 1503-1519 1483-1486

. Рафаэль "Избиение младенцев" 1509-1510


. Н. Н. Ге «Александр Сергеевич Пушкин в селе Михайловском» 1875

. Андрея Рублева «Троица» 1411-1425

. Церковь Покрова на Нерли 1165 г.
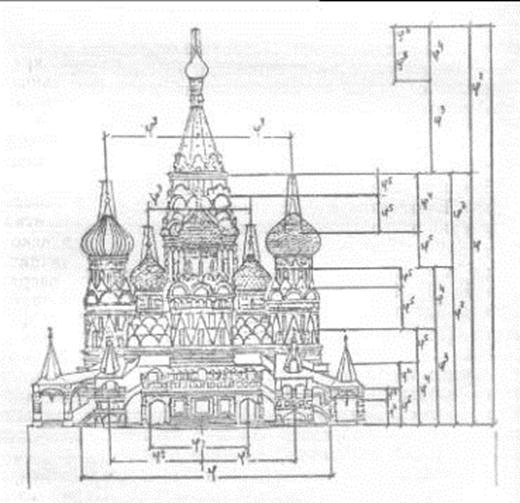
. Собор Василия Блаженного на Красной площади Москвы. 1555-1561
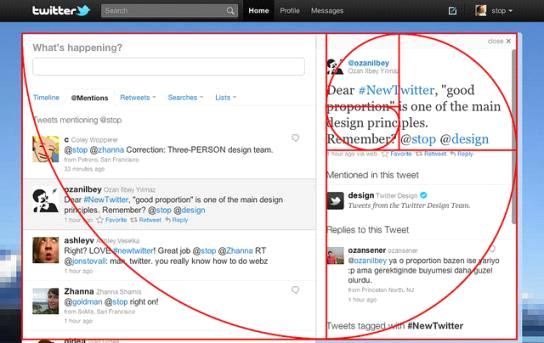
. Твиттер 2011
. Сайт It’s Numbered

. Скульптура "Золотое сечение", художник Майкл Дэвис 2010
